[ad_1]
Summary
My college trainer used to say
“All people can differentiate, however it takes an artist to combine.”
The mathematical motive behind this phrase is, that differentiation is the calculation of a restrict
$$
f'(x)=lim_{vto 0} g(v)
$$
for which we have now many guidelines and theorems at hand. And if nothing else helps, we nonetheless can draw ##f(x)## and a tangent line. Geometric integration, nonetheless, is restricted to rudimentary examples and even easy integrals such because the finite quantity of Gabriel’s horn with its infinite floor are laborious to visualise. We can not fill in a gallon of paint, however it takes infinitely many gallons to color it?!

Whereas the integrals of Gabriel’s horn
$$
textual content{quantity }=piint_1^infty dfrac{1}{x^2},dx; textual content{ and } ;textual content{floor }=2piint_1^infty dfrac{1}{x},sqrt{1+dfrac{1}{x^4}},dx
$$
can probably be solved by Riemann sums and thus with restrict calculations, too, a perform like
$$
dfrac{log x}{a+1-x}-dfrac{log x}{a+x}quad (ain mathbb{C}backslash[-1,0])
$$
which is straightforward to distinguish
$$
dfrac{d}{dx}left(dfrac{log x}{a+1-x}-dfrac{log x}{a+x}proper)=
dfrac{1}{x(a+1-x)}+dfrac{log x}{(a+1-x)^2}-dfrac{1}{x(a+x)}-dfrac{log x}{(a+x)^2}
$$
can’t be built-in straightforwardly. Earlier than I signify the most important strategies of integration which would be the content material of this text, allow us to take a look at just a little piece of artwork.
We need to discover the anti-derivative
$$
int_0^1 left(dfrac{log x}{a+1-x}-dfrac{log x}{a+x}proper),dx
$$
Outline ##F, : ,]0,1]longrightarrow mathbb{C}## by ##F(x):=dfrac{xlog x}{a+x}-log(a+x).##
Then
start{align*}
F'(x)&=dfrac{(a+x)(1+log x)-xlog x}{(a+x)^2}-dfrac{1}{a+x}=dfrac{alog x}{(a+x)^2}
finish{align*}
and
$$
aint_0^1 dfrac{log x}{(a+x)^2},dx=F(1)-F(0^+)=-log(a+1)-(-log a)=log a -log (a+1).
$$
Subsequent, we outline ##G, : ,]0,1]longrightarrow mathbb{C}## by ##G(x):=dfrac{xlog x}{a+1-x}+log(a+1-x).##
Then
start{align*}
G'(x)&=dfrac{(a+1-x)(1+log x)+xlog x}{(a+1-x)^2}-dfrac{1}{a+1-x}=dfrac{(a+1)log x}{(a+1-x)^2}
finish{align*}
and
$$
(a+1)int_0^1dfrac{log x}{(a+1-x)^2},dx=G(1)-G(0^+)=log a-log(a+1).
$$
Lastly, these integrals can be utilized to calculate
start{align*}
I(a)&=int_0^1 left(dfrac{log x}{a+1-x}-dfrac{log x}{a+x}proper),dx =int_0^1 int left(dfrac{log x}{(a+x)^2}-dfrac{log x}{(a+1-x)^2}proper),da,dx
&=int left(left(dfrac{1}{a}-dfrac{1}{a+1}proper)cdotleft(log a -log (a+1)proper)proper),da =dfrac{1}{2}left(log a -log (a+1)proper)^2+C.
finish{align*}
From ##displaystyle{lim_{a to infty}I(a)=0}## we get ##C=0## and so
$$
int_0^1 left(dfrac{log x}{a+1-x}-dfrac{log x}{a+x}proper),dx=dfrac{1}{2}left(log dfrac{a}{a+1}proper)^2.
$$
The Elementary Theorem of Calculus
If ##f:[a,b]rightarrow mathbb{R}## is a real-valued steady perform, then there exists a differentiable perform, the anti-derivative, ##F:[a,b]rightarrow mathbb{R}## such that
$$
F(x)=int_c^tf(t),dt textual content{ for }cin [a,b]textual content{ and }F'(x)=f(x)
$$
Furthermore $$int_a^b f(x),dx = left[F(x)right]_a^b=F(b)-F(a)$$
Imply Worth Theorem of Integration
$$
int_a^b f(x)g(x),dx =f(xi) int_a^b g(x),dx
$$
for a steady perform ##f:[a,b]rightarrow mathbb{R}## and an integrable perform ##g## that has no signal adjustments, i.e. ##g(x) geq 0## or ##g(x)leq 0## on ##[a,b];,,xiin [a,b].##
$$
int_a^b f(x)g(x),dx = f(a)int_a^xi g(x),dx +f(b) int_xi^b g(x),dx
$$
if ##f(x)## is monotone, ##g(x)## steady.
These theorems are extra essential for estimations of integral values than truly computing their worth.
Fubini’s Theorem
$$
int_{Xtimes Y}f(x,y),d(x,y)=int_Y int_Xf(x,y),dx,dy=int_Xint_Y f(x,y),dy,dx
$$
for steady capabilities ##f, : ,Xtimes Y rightarrow mathbb{R}.## It is likely one of the most used theorems every time an space or a quantity needs to be computed. Nevertheless, we’d like steady capabilities! An instance the place the concept can’t be utilized:
$$
underbrace{int_0^1int_0^1 dfrac{x-y}{(x+y)^3},dx,dy}_{=-1/2} =int_0^1int_0^1 dfrac{y-x}{(y+x)^3},dy,dx=-underbrace{int_0^1int_0^1dfrac{x-y}{(x+y)^3},dy,dx}_{=+1/2}
$$
Partial Fraction Decomposition
We virtually used partial fraction decomposition within the earlier instance when the issue ##dfrac{1}{a}-dfrac{1}{a+1}=dfrac{1}{a(a+1)}## within the integrand occurred. Equations like this are meant by partial fraction decomposition. Whereas ##dfrac{1}{a(a+1)}## appears troublesome to combine, the integrals of ##dfrac{1}{a}## and ##dfrac{1}{a+1}## are easy logarithms. Assume we have now polynomials ##p_k(x)## and an integrand
$$
q_0(x)prod_{okay=1}^m p_k^{-1}(x)=dfrac{q_0(x)}{prod_{okay=1}^m p_k(x)}stackrel{!}{=}sum_{okay=1}^m dfrac{q_k(x)}{p_k(x)}=sum_{okay=1}^m dfrac{q_k(x)prod_{ineq okay}p_i(x)}{prod_{okay=1}^m p_k(x)}.
$$
Then all we’d like are appropriate polynomials ##q_k(x)## such that
$$
q_0(x)=sum_{okay=1}^m q_k(x)prod_{ineq okay}p_i(x)
$$
holds and every of the ##m## many phrases is straightforward to combine. The boundaries of this system are apparent: the levels of the polynomials on the proper must be small. Partial fraction decomposition is certainly often used if the levels of ##q_k(x)## are quadratic at most, the much less the higher.
Instance: Combine ##displaystyle{int_2^{10} dfrac{x^2-x+4}{x^4-1},dx.}## This implies we have now to resolve
$$
x^2-x+4=q_1(x)underbrace{(x+1)(x-1)}_{x^2-1}+q_2(x)underbrace{(x^2+1)(x+1)}_{x^3+x^2+x+1}+q_3(x)underbrace{(x^2+1)(x-1)}_{x^3-x^2+x-1}
$$
Our unknowns are the polynomials ##q_k(x).## We set ##q_k=a_kx+b_k## and get by evaluating the coefficients
start{align*}
x^4, &: ,0= a_2+a_3
x^3, &: ,0= a_1+a_2-a_3+b_2+b_3
x^2, &: ,1= a_2+a_3+b_1+b_2-b_3
x^1, &: ,-1= -a_1+a_2-a_3+b_2+b_3
x^0, &: ,4= -b_1+b_2-b_3
finish{align*}
One answer is due to this fact ##q_1(x)=dfrac{x-3}{2}, , ,q_2(x)=x, , ,q_3(x)=-dfrac{2x+5}{2}## and
start{align*}
int_2^{10} &dfrac{x^2-x+4}{x^4-1},dx =dfrac{1}{2}int_2^{10} dfrac{x}{x^2+1},dx – dfrac{3}{2}int_2^{10} dfrac{1}{x^2+1},dx
&phantom{=}+int_2^{10}dfrac{x}{x-1},dx -int_2^{10}dfrac{x}{x+1},dx-dfrac{5}{2}int_2^{10}dfrac{1}{x+1},dx
&=dfrac{1}{4}left[phantom{dfrac{}{}}log(x^2+1)right]_2^{10}-dfrac{3}{2}left[phantom{dfrac{}{}}operatorname{arc tan}(x)right]_2^{10}
&phantom{=}+left[phantom{dfrac{}{}}x+log( x-1)right]_2^{10}-left[phantom{dfrac{}{}}x-log(x+1)right]_2^{10}-dfrac{5}{2}left[phantom{dfrac{}{}}log(x+1)right]_2^{10}
&=-dfrac{3}{2}(operatorname{arctan}(10)-operatorname{arctan}(2))+dfrac{1}{4}logleft(dfrac{101cdot 9^4cdot 3^6}{5cdot 11^6}proper)approx 0,45375ldots
finish{align*}
Integration by Components – The Leibniz Rule
Integration by elements is one other manner to take a look at the Leibniz rule.
start{align*}
(u(x)cdot v(x))’&=u(x)’cdot v(x)+u(x)cdot v(x)’
int (u(x)cdot v(x))’, dx&=int u(x)’cdot v(x),dx+int u(x)cdot v(x)’,dx
int_a^b u(x)’cdot v(x),dx &=left[u(x)v(x)right]_a^b -int_a^b u(x)cdot v(x)’,dx
finish{align*}
It’s a risk to shift the issue of integration of a product from one issue to the opposite, e.g.
start{align*}
int xlog x,dx&=dfrac{x^2}{2}log x-int dfrac{x^2}{2}cdot dfrac{1}{x},dx=dfrac{x^2}{4}left(-1+2log x proper)
finish{align*}
Integration by elements is particularly helpful for trigonometric capabilities the place we are able to use the periodicity of sine and cosine underneath differentiation, e.g.
start{align*}
int sin xcos x,dx&=-cos^2 x-int cos xsin x,dx
int sin xcos x,dx&=-dfrac{1}{2}cos^2 x=dfrac{1}{2}(-1+sin^2 x)
int cos^2 x ,dx&=x-int sin^2x,dx=x+cos xsin x-int cos^2x,dx
&=dfrac{1}{2}(x+cos xsin x)
finish{align*}
part{Integration by Discount Formulation}
Integration by elements typically gives recursions that result in so-called discount formulation since they successively lower a amount, often an exponent. Which means that an integral
$$
I_n=int f(n,x),dx
$$
could be expressed as a linear mixture of integrals ##I_k## with ##okay<n.## E.g.
start{align*}
underbrace{int x^n e^{alpha x},dx}_{=I_n}&= left[x^{n}alpha^{-1}e^{alpha x}right]-nalpha^{-1}underbrace{int x^{n-1} e^{alpha x},dx}_{=I_{n-1}}
finish{align*}
or
start{align*}
int cos^nx,dx&=left[sin xcos^{n-1}xright]+(n-1)int sin^2 xcos^{n-2}x,dx
&=left[sin xcos^{n-1}xright]+(n-1)int cos^{n-2}x,dx-(n-1)int cos^n,dx
finish{align*}
which results in the discount system
$$
int cos^nx,dx=dfrac{1}{n}left[sin xcos^{n-1}xright]+dfrac{n-1}{n}intcos^{n-2}x,dx
$$
Discount formulation could be sophisticated, and so they can have a couple of pure quantity as parameters, cp.[1]. The discount system for the sine is
$$
int sin^nx,dx=-dfrac{1}{n}left[sin^{n-1} xcos xright]+dfrac{n-1}{n}intsin^{n-2}x,dx
$$
Lobachevski’s Formulation
Let ##f(x)## be a real-valued steady perform that’s ##pi## periodic, i.e. ##f(x+pi)=f(x)=f(pi-x)## for all ##xgeq 0,## e.g. ##f(x)equiv 1.## Then
start{align*}
int_{0}^{infty }{dfrac{sin^{2}x}{x^{2}}}f(x),dx &=int_{0}^{infty }{dfrac{sin x}{x}}f(x),dx
=int_{0}^{pi /2}f(x),dx[6pt]
int_{0}^{infty }{dfrac{sin^{4}x}{x^{4}}}f(x),dx&
=int_{0}^{pi /2}f(t),dt-{dfrac{2}{3}}int_{0}^{pi /2}sin^{2}tf(t),dt
finish{align*}
This leads to the formulation
$$
int_{0}^{infty }{dfrac{sin x}{x}},dx=int_{0}^{infty }{dfrac{sin^{2}x}{x^{2}}},dx={dfrac{pi }{2}}
; textual content{ and } ; int_{0}^{infty }{dfrac{sin^{4}x}{x^{4}}},dx={dfrac{pi }{3}}.
$$
Substitutions
The Chain Rule
Substitutions are in all probability essentially the most utilized method. Barely an integral that doesn’t use it, or how I wish to put it:
Eliminate what disturbs essentially the most!
Substitution is technically a metamorphosis of the mixing variable, a change of coordinates, the chain rule!
start{align*}
int_a^b f(g(x)),dx stackrel{y=g(x)}{=}int_{g(a)}^{g(b)} f(y)cdot left(dfrac{dg(x)}{dx}proper)^{-1},dy
finish{align*}
Observe that the mixing limits change, too! After all, not any coordinate transformation is useful, and what appears as if we sophisticated issues can truly simplify the integral. We are able to take away the disturbing perform ##g(x)## every time both ##g'(x)## or ##f(x)/g'(x)## are particularly easy, e.g.
start{align*}
int_0^2 xcos (x^2+1),dxstackrel{;y=x^2+1}{=}&int_1^5 xcos ydfrac{dy}{2x}=dfrac{1}{2}int_1^5cos y,dy =dfrac{1}{2}(sin (5)-sin (1))
int_0^1sqrt{1-x^2},dxstackrel{y=arcsin x}{=}&int_{0}^{pi/2}cos^2 y,dy=left[dfrac{1}{2}(x+cos x sin x)right]_0^{pi/2}=dfrac{pi}{4}
finish{align*}
start{align*}
int_{-infty}^{infty} f(x),dfrac{tan x}{x},dx =& sum_{kin mathbb{Z}} int_{(k-1/2) pi }^{(okay+1/2)pi}f(x),dfrac{tan x}{x},dx
stackrel{y=x-kpi}{=} sum_{kin mathbb{Z}} int_{-pi /2 }^{pi /2 } f(y) ,dfrac{tan y}{y+kpi},dy
=&int_{-pi /2 }^{pi /2 }f(y)underbrace{sum_{kin mathbb{Z}} dfrac{1}{y+kpi}}_{=cot y} ,tan y, dy
stackrel{z=y+pi /2}{=} int_{0}^{pi }f(z),dz
finish{align*}
Weierstraß Substitution
The Weierstraß substitution or tangent half-angle substitution is a way that transforms trigonometric capabilities into rational polynomial capabilities. We begin with
$$
tanleft(dfrac{x}{2}proper) = t
$$
and get
$$
sin x=dfrac{2t}{1+t^2}; , ;cos x=dfrac{1-t^2}{1+t^2}; , ;
dx=dfrac{2}{1+t^2},dt.
$$
These substitutions are particularly helpful in spherical geometry. The next examples could illustrate the precept.
start{align*}
int_0^{2pi}dfrac{dx}{2+cos x}&=int_{-infty }^infty dfrac{2}{3+t^2},dtstackrel{t=usqrt{3}}{=}dfrac{2}{sqrt{3}}int_{-infty }^infty dfrac{1}{1+u^2},du=dfrac{2pi}{sqrt{3}}
finish{align*}
start{align*}
int_0^{pi} dfrac{sin(varphi)}{3cos^2(varphi)+2cos(varphi)+3},dvarphi &= int_0^infty dfrac{t}{t^4+2}~dt stackrel{u=frac{1}{2}t^2}{=}
= frac{1}{2sqrt{2}}int_0^infty dfrac{du}{1+u^2}
&= frac{1}{2sqrt{2}}left[phantom{dfrac{}{}}operatorname{arctan} u;right]_0^infty=frac{pi}{4sqrt{2}}
finish{align*}
Euler Substitutions
Euler substitutions are a way to deal with integrands which are rational expressions of sq. roots of a quadratic polynomial
$$
int Rleft(x,sqrt{ax^2+bx+c},proper),dx.
$$
Allow us to first take a look at an instance. So as to combine
$$int_1^5 dfrac{1}{sqrt{x^2+3x-4}},dx$$
we take a look at the zeros of the quadratic polynomial ##sqrt{x^2+3x-4}=sqrt{(x+4)(x-1)}.## We get from the substitution ##sqrt{(x+4)(x-1)}=(x+4)t##
$$x=dfrac{1+4t^2}{1-t^2}; , ;sqrt{x^2+3x-4}=dfrac{5t}{1-t^2}; , ;dx = dfrac{10t}{(1-t^2)^2},dt$$
start{align*}
int_1^5 frac{dx}{sqrt{x^2+3x-4}}&=int_{0}^{2/3}dfrac{2}{1-t^2},dt=int_{0}^{2/3}dfrac{1}{1+t},dt+int_{0}^{2/3}dfrac{1}{1-t},dt[6pt]
&=left[log(1+t)-log(1-t)right]_0^{2/3}=log(5)
finish{align*}
This was the third of Euler’s substitutions. All in all, we have now
- Euler’s First Substitution.
$$
sqrt{ax^2+bx+c}=pm sqrt{a}cdot x+t, , ,x=dfrac{c-t^2}{pm 2tsqrt{a}-b}; , ;a>0
$$ - Euler’s Second Substitution.
$$
sqrt{ax^2+bx+c}=xtpm sqrt{c}, , ,x=dfrac{pm 2tsqrt{c}-b}{a-t^2}; , ;c>0
$$ - Euler’s Third Substitution.
$$
sqrt{ax^2+bx+c}=sqrt{a(x-alpha)(x-beta)}=(x-alpha)t, , ,x=dfrac{abeta-alpha t^2}{a-t^2}
$$
Transformation Theorem
The chain rule works equally for capabilities in a couple of variable. Let ##Usubseteq mathbb{R}^n## be an open set and ##varphi , : ,Urightarrow mathbb{R}^n## a diffeomorphism, and ##f## an actual valued perform outlined on ##varphi(U).## Then
$$
int_{varphi(U)} f(y),dy=int_U f(varphi (x))cdot |det underbrace{(Dvarphi(x) )}_{textual content{Jacobi matrix}}|,dx.
$$
That is particularly fascinating if ##fequiv 1,## in order that the system turns into
$$
operatorname{vol}(varphi(U))=int_U |det (Dvarphi(x))|,dx = |det (Dvarphi(x))|cdotoperatorname{vol}(U),
$$
or in any instances the place the determinant equals one, e.g. for orthogonal transformations ##varphi ,## like rotations. For instance, we calculate the world beneath the Gaussian bell curve.
start{align*}
int_{-infty }^infty dfrac{1}{sigma sqrt{2pi}} e^{-frac{1}{2}left(frac{x-mu}{sigma}proper)^2},dx&stackrel{t=frac{x-mu}{sigma sqrt{2}}}{=}
dfrac{1}{sqrt{pi}} int_{-infty }^infty e^{-t^2},dtstackrel{!}{=}1
finish{align*}
As an alternative of immediately calculating the integral, we’ll present that
$$
left(int_{-infty }^infty e^{-t^2},dtright)^2=int_{-infty }^infty e^{-x^2},dx cdot int_{-infty }^infty e^{-y^2},dy=int_{-infty }^inftyint_{-infty }^infty e^{-x^2-y^2},dx,dy=pi
$$
and make use of the truth that ##f(x,y)=e^{-x^2-y^2}=e^{-r^2}## is rotation-symmetric, i.e. we’ll make use of polar coordinates. Let ##U=mathbb{R}^+occasions (0,2pi)## and ##varphi(r,alpha)=(rcos alpha,r sin alpha).##
start{align*}
det start{pmatrix}dfrac{partial varphi_1 }{partial r }&dfrac{partial varphi_1 }{partial alpha }[12pt] dfrac{partial varphi_2 }{partial r }&dfrac{partial varphi_2 }{partial alpha }finish{pmatrix}=det start{pmatrix}cos alpha &-rsin alpha sin alpha &rcos alphaend{pmatrix}=r
finish{align*}
and at last
start{align*}
int_{-infty }^inftyint_{-infty }^infty &e^{-x^2-y^2},dx,dy=int_{varphi(U)}e^{-x^2-y^2},dx,dy
&=int_U e^{-r^2cos^2alpha -r^2sin^2alpha }cdot |det(Dvarphi)(r,alpha)|,dr,dalpha
&=int_0^{2pi}int_0^infty re^{-r^2},dr,dalphastackrel{t=-r^2}{=}int_0^{2pi}dfrac{1}{2}int_{-infty }^0 e^{t},dt ,dalpha=int_0^{2pi}dfrac{1}{2},dalpha =pi
finish{align*}
Translation Invariance
$$
int_{mathbb{R}^n} f(x),dx = int_{mathbb{R}^n} f(x-c),dx
$$
is nearly self-explaining since we combine over the complete house. Nevertheless, there are much less apparent instances
$$
int_{-infty}^{infty} fleft(x-dfrac{b}{x}proper),dx=int_{-infty}^{infty}f(x),dx, textual content{ for any } ,b>0
$$
textbf{Proof:} From
$$int_{-infty}^{infty}fleft(x-dfrac{b}{x}proper),dx
stackrel{u=-b/x}{=}int_{-infty}^{infty} fleft(u-dfrac{b}{u}proper)dfrac{b}{u^2},du$$
we get
start{align*}
int_{-infty}^{infty} fleft(x-dfrac{b}{x}proper),dx &+int_{-infty}^{infty} fleft(x-dfrac{b}{x}proper),dx=int_{-infty}^{infty} fleft(x-dfrac{b}{x}proper)left(1+dfrac{b}{x^2}proper),dx
&= int_{-infty}^{0} fleft(x-dfrac{b}{x}proper)left(1+dfrac{b}{x^2}proper),dx +int_{0}^{infty} fleft(x-dfrac{b}{x}proper)left(1+dfrac{b}{x^2}proper),dx
&stackrel{v=x-(b/x)}{=} int_{-infty}^{infty} f(v),dv +int_{-infty}^{infty} f(v),dv=2int_{-infty}^{infty} f(v),dv
finish{align*}
which proves the assertion.
Symmetries
Symmetries are the core of arithmetic and physics generally. So it doesn’t shock that they play an important position in integration, too. The precept is a simplification:
$$
int_{-c}^c |x|,dx= 2cdot int_0^c x,dx = c^2
$$
Additive Symmetry
A bit extra subtle instance for additive symmetry is ##displaystyle{int_0^{pi/2}}log (sin(x)),dx.##
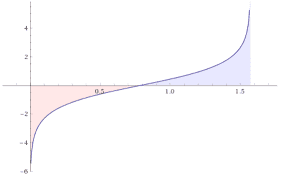
We use the symmetry between the sine and cosine capabilities.
start{align*}
int_0^{pi/2}log (sin x),dx&=-int_{pi/2}^0log (cos x),dx=int_0^{pi/2}log (cos x),dx
finish{align*}
start{align*}
2int_0^{pi/2}log (sin x),dx&=int_0^{pi/2}log (sin x),dx+int_0^{pi/2}log (cos x ,dx
&=int_0^{pi/2}log(sin x cos x)=int_0^{pi/2}logleft(dfrac{sin 2x}{2}proper),dx
&stackrel{u=2x}{=}-dfrac{pi}{2}log 2+dfrac{1}{2}int_0^{pi}log(sin u),du
&=-dfrac{pi}{2}log 2+int_0^{pi/2}log(sin u),du
finish{align*}
We thus have ##displaystyle{int_0^{pi/2}log (sin x),dx=-dfrac{pi}{2}log 2.}##
We are able to in fact calculate symmetric areas. That simplifies the mixing boundaries.

The world of an astroid is enclosed by ##(x,y)=(cos^3 t,sin^3 t)## for ##0leq t leq 2pi.##
$$
4int_0^1 y,dxstackrel{x=cos^3(t)}{=}-12int_{pi/2}^0 sin^4 tcdot cos^2 t ,dt = dfrac{3}{8}pi
$$
Multiplicative Symmetry
A bit much less well-known are probably the multiplicative symmetries. We virtually bumped into one within the instance within the translation paragraph earlier than it lastly turned out to be an additive symmetry. Let’s illustrate with some examples what we imply, e.g. with a multiplicative asymmetry.
$$
int_0^pilog(1-2alpha cos(x)+alpha^2),dx=2pilog |alpha|; , ;|alpha|geq 1
$$
however how can we all know? We begin with a worth ##|alpha|leq 1## and ##0<x<pi.## Then by Gradshteyn, Ryzhik 1.514 [6]
$$
log(1-2alpha cos(x)+alpha^2)= -2sum_{okay=1}^{infty}dfrac{cos(kx)}{okay},alpha^okay
$$
and
##displaystyle{I(alpha)=int_0^pi log (1-2alpha cos(x)+alpha^2),dx = -2sum_{okay=1}^{infty} dfrac{alpha^okay}{okay} int_{0}^{pi} cos(kx),dx =0}.##
This implies for ##|alpha|geq 1##
start{align*}
int_0^pi log (1-2alpha cos(x)+alpha^2),dx &= int_0^pi logleft(alpha^2 left(dfrac{1}{alpha^2}-dfrac{2}{alpha}cos(x)+1right)proper),dx
&=2pi log|alpha| + underbrace{Ileft(dfrac{1}{alpha}proper)}_{=0}= 2pi log|alpha|
finish{align*}
So we used a consequence about ##I(1/a)## to calculate ##I(a).## The following instance makes use of the multiplicative symmetry of the mixing variable
start{align*}
int_{n^{-1}}^{n} fleft(x+dfrac{1}{x}proper),dfrac{log x}{x},dx &stackrel{y=1/x}{=} int_{n}^{n^{-1}}fleft(dfrac{1}{y}+yright),dfrac{log y}{y},dy
&=-int_{n^{-1}}^{n} fleft(x+dfrac{1}{x}proper),dfrac{log x}{x},dx
finish{align*}
which is barely potential if the mixing worth is zero. By comparable arguments
$$
int_{frac{1}{2}}^{3} dfrac{1}{sqrt{x^2+1}},dfrac{log(x)}{sqrt{x}},dx , + , int_{frac{1}{3}}^{2} dfrac{1}{sqrt{x^2+1}},dfrac{log(x)}{sqrt{x}},dx =0
$$
and
$$
int_{pi^{-1}}^pi dfrac{1}{x}sin^2 left( -x-dfrac{1}{x} proper) log x,dx=0
$$
Including an Integral
It’s typically useful to rewrite an integrand with a further integral, e.g. for ##alphanotin mathbb{Z}##
start{align*}
int_0^infty dfrac{dx}{(1+x)x^alpha} &= int_0^infty x^{-alpha} int_0^infty e^{-(1+x)t},dt,dx=int_0^inftyint_0^infty x^{-alpha} e^{-t}e^{-xt},dt,dx
&stackrel{u=tx}{=}int_0^inftyint_0^infty left(dfrac{u}{t}proper)^{-alpha}e^{-u}e^{-t}t^{-1},du,dx
&=int_0^infty u^{-alpha}e^{-u},du, int_0^infty t^{alpha -1} e^{-t},dt=Gamma (1-alpha) Gamma(alpha)=dfrac{pi}{sin pi alpha}
finish{align*}
or
start{align*}
&int_0^infty frac{x^{m}}{x^{n} + 1}dx = int_0^infty x^{m} int_0^infty e^{-x^n y} e^{-y} ,dy, dx
&stackrel{z=x^ny}{=}dfrac{1}{n} int_0^infty e^{-y} left(frac{1}{y}proper)^frac{m+1}{n} ,dy int_0^infty e^{-z} z^frac{m-n+1}{n} ,dz= dfrac{Gammaleft(dfrac{n-m-1}{n}proper) Gammaleft(dfrac{m+1}{n}proper)}{n}
finish{align*}
The Mass at Infinity
If ##f_k: Xrightarrow mathbb{R}## is a sequence of pointwise absolute convergent, integrable capabilities, then
$$
int_X left(sum_{okay=1}^infty f_k(x)proper),dx=sum_{okay=1}^infty left(int_X f_k(x),dxright)
$$
Instance: The Wallis Collection.
start{align*}
int_0^{pi/2}dfrac{2sin x}{2-sin^2 x},dx&=int_0^{pi/2}dfrac{2sin x}{1+cos x},dx=left[-2arctan(cos x)right]_0^{pi/2}=dfrac{pi}{2}
&=int_0^{pi/2}dfrac{sin x}{1-frac{1}{2}sin^2 x},dx=int_0^{pi/2}sum_{okay=0}^infty 2^{-k}sin^{2k+1}x ,dx
&=sum_{okay=0}^inftyint_0^{pi/2}2^{-k}sin^{2k+1}x ,dx=sum_{okay=0}^inftydfrac{1cdot 2cdot 3cdots okay}{3cdot 5 cdot 7 cdots (2k+1)}
finish{align*}
Absolutely the convergence is essential as we are able to see within the following instance. Let ##f_k=I_{[k,k+1,]}-I_{[k+1,k+2]}## with the indicator perform ##I_{[k,k+1,]}(x)=1## if ##xin[k,k+1]## and ##I_{[k,k+1,]}(x)=0## in any other case. If we sum up these capabilities, we get a telescope impact. The bump at ##[0,1]## stays untouched whereas the bump (the mass) ##[k+1,k+2]## escapes to infinity: ##displaystyle{sum_{okay=0}^n}f_k=I_{[0,1,]}-I_{[n+1,n+2]}## and ##displaystyle{sum_{okay=1}^infty f_k(x)}=I_{[0,1,]}(x).## Therefore,
$$
1=int_mathbb{R}I_{[0,1,]}(x),dx=int_mathbb{R} left(sum_{okay=1}^infty f_k(x)proper),dxneq sum_{okay=1}^infty left(int_mathbb{R} f_k(x),dxright)=0.
$$
Limits and Integrals
Mass at infinity is strictly an alternate of a restrict and an integral. So what about limits generally? Even when all capabilities ##f_k## of a convergent sequence are steady or integrable, the identical shouldn’t be essentially true for the restrict. Have a look at
$$
f_k(x)=start{instances}okay^2x &textual content{ if }0leq xleq 1/okay 1/x&textual content{ if }1/kleq xleq 1end{instances}
$$
Each perform is steady and due to this fact integrable, however the restrict ##displaystyle{lim_{okay to infty}f_k(x)=dfrac{1}{x}}## is neither. Even when all ##f_k## and the restrict perform ##f## are integrable, their integrals don’t have to match, e.g.
$$
triangle_r(x)=start{instances}0 &textual content{ if }|x|geq r dfracx{r^2}&textual content{ if }|x|leq rend{instances}; , ;lim_{r to 0}triangle_r(x)=triangle_0(x):=start{instances}infty &textual content{ if }x=0�&textual content{ if }xneq 0end{instances}
$$
We thus have
$$
lim_{r to 0}inttriangle_r(x),dx =lim_{r to 0} 1=1neq 0=int triangle_0,dx=intlim_{r to 0}triangle_r(x),dx
$$
Once more, the mass escapes to infinity. To forestall this from occurring, we’d like an integrable perform as an higher certain.
Let ##f_0,f_1,f_2,ldots## be a sequence of actual integrable capabilities that converge pointwise to ##displaystyle{lim_{okay to infty}f_k(x)}=f(x).## If their is an actual integrable perform ##h(x)## such that ##|f_k|leq h## and ##int h(x),dx <infty ,## then ##f## is integrable and
$$
displaystyle{lim_{okay to infty}int f_k(x),dx=int lim_{okay to infty}f_k(x),dx=int f(x),dx}
$$
The thought behind the proof is straightforward. We get from ##|f_k|leq h## that ##|f|leq h## and so ##|f-f_k|leq|f|+|f_k|leq 2h.## By Fatou’s lemma, we have now
start{align*}
int 2h&=int liminfleft(2h-|f_k-f|proper)leq liminfintleft(2h-|f_k-f|proper)
&=liminfleft(int 2h-int |f_k-f|proper)=int 2h-limsupint|f_k-f|
finish{align*}
Since ##int h<infty ,## we conclude ##lim int|f_k-f|=0.##
Instance: The Stirling Formulation.
$$
lim_{n to infty}dfrac{n!}{sqrt{n}left(frac{n}{e}proper)^n}=sqrt{2pi}
$$
We use the ability collection of the logarithm for ##|s|<1##
$$
log(1+s)=s-dfrac{s^2}{2}+dfrac{s^3}{3}-dfrac{s^4}{4}pm ldots
$$
and get for ##s=t/sqrt{n}## with ##-sqrt{n}<t<sqrt{n}##
$$
nleft(logleft(1+dfrac{t}{sqrt{n}}proper)-dfrac{t}{sqrt{n}}proper)=-dfrac{t^2}{2}+dfrac{t^3}{sqrt{n}}-dfrac{t^4}{4n}pmldotsstackrel{nto infty }{longrightarrow }-dfrac{t^2}{2}
$$
We additional know that
$$
n!=Gamma(n+1)=int_0^infty x^ne^{-x},dx
$$
so we get
start{align*}
dfrac{n!}{sqrt{n}left(frac{n}{e}proper)^n}=&int_0^infty
expleft(nleft(logleft(dfrac{x}{n}proper)+1-dfrac{x}{n}proper)proper),dfrac{dx}{sqrt{n}}
stackrel{x=sqrt{n}t+n}{=}&int_{-sqrt{n}}^{infty }exp
left(nleft(logleft(1+dfrac{t}{sqrt{n}}proper)-dfrac{t}{sqrt{n}}proper)proper),dt
=&int_{-infty }^infty underbrace{exp
left(nleft(logleft(1+dfrac{t}{sqrt{n}}proper)-dfrac{t}{sqrt{n}}proper)proper)cdot I_{ [-sqrt{n},infty [ }}_{=f_n(t)},dt
end{align*}
We saw that the sequence ##f_n(t)## converges pointwise to ##e^{-t^2/2},## is integrable and bounded from above by an integrable function. Hence, we can switch limit and integration.
$$
lim_{n to infty}dfrac{n!}{sqrt{n}left(frac{n}{e}right)^n}=lim_{n to infty}int_mathbb{R}f_n(t),dt=int_mathbb{R}lim_{n to infty}f_n(t),dt=int_mathbb{R}e^{-t^2/2},dt = sqrt{2pi}
$$
The Feynman Trick – Parameter Integrals
“Then I come along and try differentiating under the integral sign, and often it worked. So I got a great reputation for doing integrals, only because my box of tools was different from everybody else’s, and they had tried all their tools on it before giving the problem to me.” (Richard Feynman, 1918-1988)
$$
dfrac{d}{dx}int f(x,y),dy stackrel{(*)}{=}int dfrac{partial }{partial x}f(x,y),dy
$$
Let us consider an example and define ##f(x,y)=xcdot |x|cdot e^{-x^2y^2}.## Therefore
begin{align*}
dfrac{d}{dx}int_mathbb{R} f(x,y),dy&=dfrac{d}{dx}int_mathbb{R}x |x| e^{-x^2y^2}stackrel{t=xy}{=}dfrac{d}{dx}xint_mathbb{R}e^{-t^2},dt=sqrt{pi}[6pt]
int_mathbb{R} dfrac{partial }{partial x}f(x,y),dy&=int_mathbb{R} dfrac{partial }{partial x}x |x| e^{-x^2y^2},dy=2int_mathbb{R}left(|x|e^{-x^2y^2}- |x|x^2y^2 e^{-x^2y^2}proper),dy[6pt]
&stackrel{t=xy, , ,xneq 0}{=}2 int_mathbb{R}e^{-t^2},dt -2 int_mathbb{R}t^2e^{-t^2},dt =2sqrt{pi}-2dfrac{sqrt{pi}}{2}=sqrt{pi}
finish{align*}
This exhibits us that differentiation underneath the integral works fantastic for ##xneq 0## whereas at ##x=0## we have now
$$
sqrt{pi}=dfrac{d}{dx}int xcdot |x|cdot e^{-x^2y^2},dy neqint dfrac{partial }{partial x}xcdot |x|cdot e^{-x^2y^2},dy=0
$$
The lacking situation is
$$
(*)qquad … textual content{ if }f(x,y)textual content{ is textbf{repeatedly differentiable} alongside the parameter }x.
$$
Residues
Residue calculus deserves an article by itself, see [7]. So we’ll solely give just a few examples right here. Residue calculus is the artwork of fixing actual integrals (and complicated integrals) by utilizing advanced capabilities and numerous theorems of Augustin-Louis Cauchy.
Let ##f(z)## be an analytic perform ##f(z)## with a pole at ##z_0## and
$$f(z)=sum_{n=-infty }^infty a_n (z-z_0)^n; , ;a_n=displaystyle{dfrac{1}{2pi i} oint_{partial D_rho(z_0)} dfrac{f(zeta)}{(zeta-z_0)^{n+1}},dzeta}$$ be the Laurent collection of ##f(z)## on a disc with radius ##rho## round ##z_0.## The coefficient at ##n=-1## is named the residue of ##f## at ##z_0,##
$$
operatorname{Res}_{z_0}(f)=a_{-1}=dfrac{1}{2pi i} oint_{partial D_rho(z_0)} f(zeta) ,dzeta.
$$
Mellin-Transformation.
$$
int_0^infty x^{lambda -1}R(x),dx=dfrac{pi}{sin(lambda pi)}sum_{z_k}operatorname{Res}_{z_k}left(fright); , ;lambda in mathbb{R}^+backslash mathbb{Z}
$$
the place ##R(x)=p(x)/q(x)## with ##p(x),q(x)in mathbb{R}[x],## ##q(x)neq 0 textual content{ for }xin mathbb{R}^+,## ##q(z_k)=0## for poles ##z_kin mathbb{C}## and the integral exists, i.e. ##lambda +deg p<deg q.##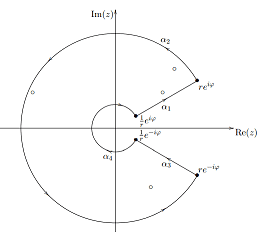 Observe that
Observe that
$$
f(z),dx:={(-z)}^{lambda -1}R(z)=expleft((lambda -1)log(-z)proper)R(z)
$$
is holomorphic for ##zin mathbb{C}backslash mathbb{R}^+## if we selected the primary department of the advanced logarithm. We outline a closed curve
$$
alpha=start{instances}
alpha_1(t)=te^{ivarphi }&textual content{ if } tin left[1/r,rright]
alpha_2(t)=re^{it}&textual content{ if }t inleft[varphi ,2pi -varphi right]
alpha_3(t)=-te^{-ivarphi }&textual content{ if }tin left[-r,-1/rright]
alpha_4(t)=frac{1}{r}e^{i (2pi-t)}&textual content{ if }tin left[varphi ,2pi – varphi right]
finish{instances}
$$
such that the poles are all enclosed by ##alpha## for giant sufficient ##r## and sufficiently small ##varphi## and
$$
int_{alpha_1}f(z),dz+underbrace{int_{alpha_2}f(z),dz}_{stackrel{varphi to 0}{longrightarrow },0}+int_{alpha_3}f(z),dz+underbrace{int_{alpha_4}f(z),dz}_{stackrel{varphi to 0}{longrightarrow },0}=2pi i sum_{z_k}operatorname{Res}_{z_k}left(fright)
$$
We are able to present that
start{align*}
displaystyle{lim_{varphi to 0}}&int_{alpha_1}f(z),dz=-e^{-lambda pi i}int_{1/r}^r t^{lambda -1}R(t),dt
displaystyle{lim_{varphi to 0}}&int_{alpha_3}f(z),dz=e^{lambda pi i}int_{1/r}^r t^{lambda -1}R(t),dt
finish{align*}
and at last get
$$
2pi i sum_{z_k}operatorname{Res}_{z_k}left(fright) =lim_{r to infty}int_alpha f(t),dt=2 i sin(lambda pi) int_{-infty }^infty t^{lambda -1}R(t),dt.
$$
The sinc Perform.
The sinc perform is outlined as ##operatorname{sinc}(x)=dfrac{sin x}{x}## for ##xneq 0## and ##operatorname{sinc(0)=1}.##
start{align*}
int_0^infty dfrac{sin x}{x},dx&=dfrac{1}{2}lim_{r to infty}int_{-r}^rdfrac{e^{iz}-e^{-iz}}{2i z},dz=operatorname{Res}_0left(dfrac{e^{iz}}{4 i z}proper)=dfrac{pi}{2}
finish{align*}
Guidelines for Residues.
We lastly embrace some common calculation guidelines for residue calculus that we took from [7].
$$
start{array}{ll} operatorname{Res}_{z_0}(alpha f+beta g)=alphaoperatorname{Res}_{z_0}(f)+betaoperatorname{Res}_{z_0}(g) &(z_0in G , , ,alpha, beta in mathbb{C}) [16pt] operatorname{Res}_{z_1}left(dfrac{h}{f}proper)=dfrac{h(z_1)}{f'(z_1)}& operatorname{Res}_{z_1}left(dfrac{1}{f}proper)=dfrac{1}{f'(z_1)}[16pt] operatorname{Res}_{z_m}left(hdfrac{f’}{f}proper)=h(z_m)cdot m&operatorname{Res}_{z_m}left(dfrac{f’}{f}proper)=m[16pt] operatorname{Res}_{p_1}(hcdot f)=h(p_1)cdot operatorname{Res}_{p_1}(f)&operatorname{Res}_{p_1}(f)=displaystyle{lim_{z to p_1}((z-p_1)f(z))}[16pt] operatorname{Res}_{p_m}(f)=dfrac{1}{(m-1)!}displaystyle{lim_{z to p_m}dfrac{partial^{m-1} }{partial z^{m-1}}left( (z-p_m)^m f(z) proper)}&operatorname{Res}_{p_m}left(dfrac{f’}{f}proper)=-m[16pt] operatorname{Res}_{infty }(f)=operatorname{Res}_0left(-dfrac{1}{z^2}fleft(dfrac{1}{z}proper)proper)&operatorname{Res}_{p_m}left(hdfrac{f’}{f}proper)=-h(p_m)cdot m[16pt] operatorname{Res}_{z_0}(h)=0 & operatorname{Res}_0left(dfrac{1}{z}proper)=1[16pt] operatorname{Res}_1left(dfrac{z}{z^2-1}proper)=operatorname{Res}_{-1}left(dfrac{z}{z^2-1}proper)=dfrac{1}{2}&operatorname{Res}_0left(dfrac{e^z}{z^m}proper)=dfrac{1}{(m-1)!}
finish{array}
$$
Sources
[ad_2]



